Зависимость тока в проводнике от напряжения на его концах. Электрическое сопротивление проводника.

Проведём эксперимент, для этого соединим источник тока с проводником (резистором), к которому последовательно подключим амперметр (для измерения силы тока на резисторе), а параллельно – вольтметр (для измерения напряжения на резисторе) (см. Рис. 1). Первоначально, при напряжении 1 В, сила тока равна 1 А. При увеличении напряжения в 2 раза, до 2 В, сила тока увеличилась также в 2 раза (2 А) (см. Рис. 2).

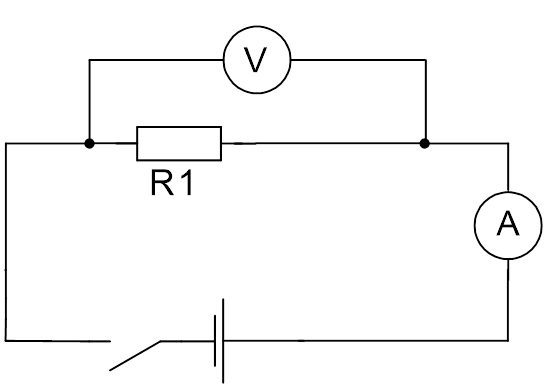
Рис. 1. Электрическая схема для эксперимента

Из опыта видно, что при увеличении или уменьшении напряжения на концах проводника во столько же раз увеличится или уменьшится сила тока в проводнике. Такую зависимость впервые экспериментально получил немецкий учёный Георг Ом в 1826 году. Из курса математики известно, что её можно записать в таком виде:

,

где I – сила тока; U – напряжение; k – коэффициент пропорциональности.

Представим зависимость в виде графика (см. Рис. 3). Такой график зависимости силы тока в проводнике от напряжения на его концах называют вольтамперной характеристикой (также может быть представлена в виде таблицы).

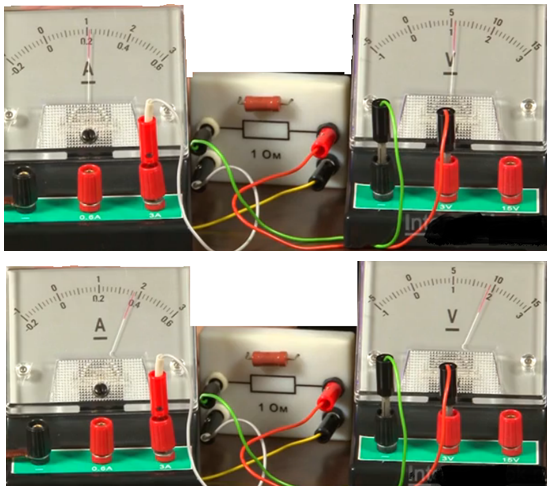
Рис. 2. Показания амперметра при изменении напряжения

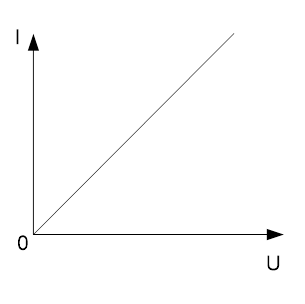
Рис. 3. Вольтамперная характеристика проводника

Для следующего эксперимента соберём электрическую схему аналогично предыдущему, заменив в ней проводник (см. Рис. 4).  Первоначально, при напряжении около 1,5 В, сила тока равна примерно 0,3 А. При увеличении напряжения до 3 В, сила тока увеличится примерно до 0,6 А (см. Рис. 5).

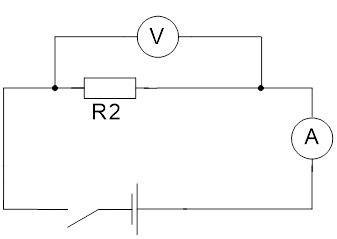
Рис. 4. Электрическая схема для эксперимента

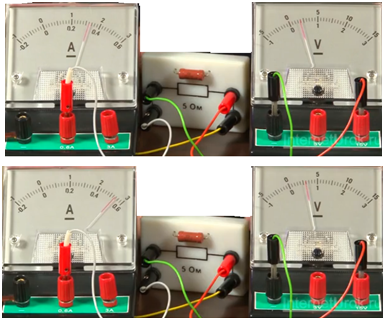
Рис. 5. Показания амперметра при изменении напряжения

Проведя опыты с различными проводниками, установили, что сила тока в проводнике всегда пропорциональна напряжению на его концах, при этом коэффициент пропорциональности зависит от проводника. Таким образом, сила тока в проводнике зависит не только от напряжения на его концах, но и от свойства проводника. То есть зависимость  можно записать так:

 или ,

где R – электрическое сопротивление проводника.

Величина  – проводимость. Единица измерения проводимости называется сименсом (См), названная в честь немецкого физика Эрнеста Сименса. 1 См – электрическая проводимость проводника с сопротивлением 1 Ом.

При одинаковом напряжении на концах проводников, сила тока меньше в том проводнике, который обладает большим сопротивлением. То есть чем больше сопротивление проводника, тем сильнее проводник противодействует прохождению тока. При этом часть электрической энергии превращается во внутреннюю энергию проводника.

Электрическое сопротивление – это физическая величина, характеризующая свойство проводника противодействовать электрическому току. Единица сопротивления в СИ – Ом.

1 Ом – это сопротивление проводника, в котором при напряжении на концах 1 В сила тока равна 1 А.

Закон Ома для неоднородного участка цепи

При прохождении электрического тока в замкнутой цепи на свободные заряды действуют силы со стороны стационарного электрического поля и сторонние силы. При этом на отдельных участках этой цепи ток создается только стационарным электрическим полем. Такие участки цепи называются однородными. На некоторых участках этой цепи, кроме сил стационарного электрического поля, действуют и сторонние силы. Участок цепи, на котором действуют сторонние силы, называют неоднородным участком цепи.

Для того чтобы выяснить, от чего зависит сила тока на этих участках, необходимо уточнить понятие напряжения.

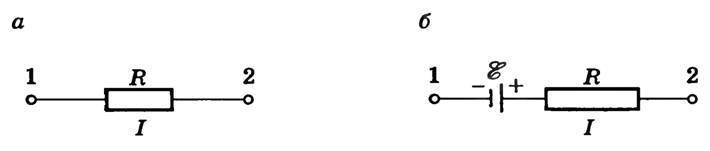
Рассмотрим вначале однородный участок цепи (рис. 1, а). В этом случае работу по перемещению заряда совершают только силы стационарного электрического поля, и этот участок характеризуют разностью потенциалов Δφ. Разность потенциалов на концах участка \(~\Delta \varphi = \varphi_1 — \varphi_2 = \frac{A_K}{q}\), где A_K — работа сил стационарного электрического поля. Неоднородный участок цепи (рис. 1, б) содержит в отличие от однородного участка источник ЭДС, и к работе сил электростатического поля на этом участке добавляется работа сторонних сил. По определению, \(~\frac{A_{el}}{q} = \varphi_1 — \varphi_2\), где q — положительный заряд, который перемещается между любыми двумя точками цепи; \(~\varphi_1 — \varphi_2\) — разность потенциалов точек в начале и конце рассматриваемого участка; \(~\frac{A_{st}}{q} = \varepsilon\). Тогда говорят о напряжении для напряженности: E_{стац. э. п.} = E_{э/стат. п.} + E_стор. Напряжение U на участке цепи представляет собой физическую скалярную величину, равную суммарной работе сторонних сил и сил электростатического поля по перемещению единичного положительного заряда на этом участке:

Из этой формулы видно, что в общем случае напряжение на данном участке цепи равно алгебраической сумме разности потенциалов и ЭДС на этом участке. Если же на участке действуют только электрические силы (ε = 0), то \(~U = \varphi_1 — \varphi_2\). Таким образом, только для однородного участка цепи понятия напряжения и разности потенциалов совпадают.

Закон Ома для неоднородного участка цепи имеет вид:

где R — общее сопротивление неоднородного участка.

ЭДС ε может быть как положительной, так и отрицательной. Это связано с полярностью включения ЭДС в участок: если направление, создаваемое источником тока, совпадает с направлением тока, проходящего в участке (направление тока на участке совпадает внутри источника с направлением от отрицательного полюса к положительному), т.е. ЭДС способствует движению положительных зарядов в данном направлении, то ε > 0, в противном случае, если ЭДС препятствует движению положительных зарядов в данном направлении, то ε