Форма

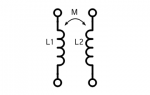
На рисунке слева — Ш-образный сердечник, справа — П-образный. A — толщина сердечника, B — высота окна сердечника, C — ширина окна сердечника, D — ширина зуба.

Делая прокладку в сердечнике, не забудьте, что ее толщина должна быть вдвое меньше расчетного зазора, так как магнитная линия в Ш и П — образных сердечниках пересекает ее дважды.

(читать дальше…) :: (в начало статьи)

:: ПоискТехника безопасности :: Помощь

К сожалению в статьях периодически встречаются ошибки, они исправляются, статьи дополняются, развиваются, готовятся новые. Подпишитесь, на новости, чтобы быть в курсе.

Если что-то непонятно, обязательно спросите!Задать вопрос. Обсуждение статьи. сообщений.

Доброго дня. Можно ли применить методику для расчета моторного трехфазного дросселя (ПЧ+двигатель)? Какие особенности изготовления таких дросселей (например, взять три трансформатора и пр.)? Читать ответ…

Доброго здравия! По какой формуле включается предупреждение о недостаточности мощности сердечника? Читать ответ…

Здравствуйте! Я собираю сварочный инвертор по схеме из книги Негуляева (полумост резонансный), и пытался определить с помощью ваших онлайн-калькуляторов индуктивность дросселя резонанса, но в них надо подставлять известное значение индуктивности (и откуда, к слову, его взять если нет измерительных приборов) и получать витки. А мне то надо наоборот. Это нужно, чтобы попытать Читать ответ…

В расчёте дросселя, а именно определении зазора, есть расхождения около 30% в меньшую сторону. Как можете это прокомментировать. Читать ответ…

При токе 50-60 А на Ш образном сердечнике витки, расположенные в непосредственной близости к зазору начинают обугливаться. Любая железка, введённая в зазор просто плавится. Это же индукционка какая-то получается. Практика подсказывает, нужно как можно дальше удалять витки от зазора. Предпочтение в таких случаях отдаётся П — обр. сердечникам. Так ли это? Читать ответ…

Помимо непонятного выражения в формуле зазора, еще непонятно почему в других источниках приведены, кажется, какие-то иные расчеты? Вот например, в этой книге , я так понял, какой-то общий случай расчета, или почему-то другие они. Читать ответ…

Здравствуйте. А что значит выражение в формуле величины зазора в сердечнике? Читать ответ…

Спасибо за материал!
‘Провод 0.25мм’ — это диаметр или площадь сечения? Читать ответ…

Здравствуйте. Для сборки импульсного источника синусоидального напряжения расчитываю параметры дросселя L1. Имеющийся Ш-образный сердечник 20*28 N87 мал по размерам, как указывает онлайн расчет. Но в программе нет возможности по требуемым параметрам подобрать необходимый размер. Чтобы пойти и купить нужный. Подскажите или требуемые габаритные размеры или программку для выбора Читать ответ…

Здравствуйте, не могли бы вы помочь с расчётом дросселя для схемы опубликованной на вашем сайте: http://hw4.ru/circuitry-switching-sinus

В наличие имеется провод диаметром 0,5мм и ферритовые кольца B64290L0651X03
http://static.advonics.com/content/pdfs/221/7092193.pdf

Размер R22,1×13,7×12,5(mm)
Материал Т38
Начальная проницаемость 10 000

Номинальный вы Читать ответ…

Еще статьи

Изготовление дросселя, катушки индуктивности своими руками, самому, са…
Расчет и изготовление катушки индуктивности, дросселя. Типовые электронные схемы…

Силовой мощный импульсный трансформатор, дроссель. Намотка. Изготовить…
Приемы намотки импульсного дросселя / трансформатора….

Импульсный источник питания. Своими руками. Самодельный. Сделать. Лабо…
Схема импульсного блока питания. Расчет на разные напряжения и токи….

Конструирование (проектирование и расчет) источников питания и преобра…
Разработка источников питания и преобразователей напряжения. Типовые схемы. Прим…

Проверка дросселя, катушки индуктивности, трансформатора, обмотки, эле…
Как проверить дроссель, обмотки трансформатора, катушки индуктивности, электрома…

Практика проектирования электронных схем. Самоучитель электроники….
Искусство разработки устройств. Элементная база радиоэлектроники. Типовые схемы….

Пушпульный импульсный источник питания. Онлайн расчет. Форма. Подавлен…
Как рассчитать пуш-пульный импульсный преобразователь напряжения. Как подавить п…

Повышающий импульсный источник питания. Онлайн расчет. Форма. Подавлен…
Как рассчитать повышающий импульсный преобразователь напряжения. Как подавить пу…

Методы расчета индуктивностей

Наиболее полно теоретические основы методов расчета индуктивностей изложены в справочной книге: «». Здесь же хотелось бы немного систематизировать подходы к расчету индуктивностей.

Прежде всего отметим, что расчет индуктивности можно вести двумя способами:∙ Численный метод с различной степенью упрощения задачи ∙ Расчет по упрощенным эмпирическим формулам

Эмпирический подход предполагает подбор (подгонку) относительно несложных аппроксимирующих формул по результатам измерений индуктивности реальных катушек. Расчет по упрощенным эмпирическим формулам имеет ограничения в точности и применим только к катушкам с определенной геометрией намотки. Большинство таких формул можно найти здесь. Несмотря на невысокую точность, такой расчет чаще всего вполне достаточен в радиолюбительской практике.

Численные методы основываются на реальных физических моделях катушек индуктивности и их, в свою очередь, можно разбить на две категории:

1. Расчет в программах основанных на фундаментальных законах классической электродинамики, так называемых электромагнитных симуляторах. К ним можно отнести , , , и т.п. Эти программы используют специальные численные методы, такие как и . Расчет в таких программах довольно точен, позволяет учесть множество нюансов, рассчитать катушку произвольной формы, однако требует огромных ресурсов компьютера. Применяется при научном анализе или если катушка работает в режиме, когда ее нельзя представлять как сосредоточенный элемент []
2. Численные методы расчета, основанные на фундаментальных формулах физики, применимых к круговым проводникам, выведенных в XIX веке . Позволяют провести расчет более точно, чем по эмпирическим формулам, но не требуют запредельных аппаратных ресурсов компьютера. На них следует остановится подробнее, т.к их и использует Coil32…

Расчет индуктивности в программе Coil32 основан на модели Максвелла, в которой катушка представляется как множество соосных бесконечно тонких круговых проводников.Из следует, что силовые линии магнитного поля всегда замкнуты. Из этого следует, что магнитный поток порожденный круговым контуром с током весь проходит через поверхность, ограниченную этим контуром. Это обстоятельство отражено в следующей формуле:

Из этой формулы можно вывести определение для собственной индуктивности кругового проводника через двойной контурный интеграл Ф.Е.Неймана для взаимоиндукции :

Как показал Д.К.Максвелл, для двух бесконечно тонких круговых соосных проводников этот интеграл имеет однозначное решение, которое выглядит следующим образом:

, где:

• M — взаимоиндукция;
• r₁, r₂ — радиусы двух бесконечно тонких круговых проводников;
• x — расстояние между центрами кругов, ограниченных этими проводниками;
• K,E — , соответственно первого и второго рода;

Численный метод расчета по формуле Максвелла сводится к численным методам решения эллиптических интегралов.

По формуле Максвелла можно рассчитывать как индуктивность многослойных и однослойных катушек, так и взаимную индуктивность двух отдельных катушек. Погрешности модели, связанные с допущением, что провод бесконечно тонкий и представляет собой набор круговых проводников (хотя на самом деле — это спираль), можно уменьшить с помощью соответствующих поправок.

Рассчитывая взаимоиндукцию проводника «самого на себя», т.е. его самоиндукцию (собственную индуктивность), Максвелл использует понятие — «среднее геометрическое расстояние» — GDM (g), для круглого провода:

g = e0.25*r_w, где r_w — радиус провода.

Очень важен следующий момент. Вся вышеприведенная логика рассуждений и вывода формул, начиная от формулы Неймана, справедлива в случае равномерного распределения плотности тока вдоль катушки. В подавляющем большинстве практических случаев так и есть. Однако если катушка работает вблизи частот собственного резонанса, начинает проявляться неравномерность распределения плотности тока по проводнику! Другими словами, начинает проявляться зависимость индуктивности от частоты, которая в наших расчетах не учитывается. Поэтому индуктивность катушки можно рассчитать корректно только на частотах не превышающих 60-70% от частоты ее собственного резонанса. Таким образом Coil32 не годится для точных расчетов, например, катушек Тесла или спиральных резонаторов. В этом случае и в случае если катушка работает в режиме выше частоты собственного резонанса — ее нужно представлять только в виде модели длинной линии и рассчитывать в программах-электромагнитных симуляторах, либо пользоваться специальными эмпирическими формулами.

Ссылки:

1. D W Knight 2013
2. Robert Weaver 2012
3. Marc T. Thompson 1999
4. M.A.Bueno A K T Assis 1995

Эквивалентная схема реальной катушки индуктивности

В этом калькуляторе мы рассматривали идеальную катушку индуктивности. В то же время, в реальной жизни таких катушке не бывает. Катушки обычно конструируются с минимальными размерами таким образом, чтобы они помещались в миниатюрное устройство. Любую реальную катушку индуктивности можно представить в виде идеальной индуктивности, к которой параллельно подключены емкость и сопротивление, а еще одно сопротивление подключено последовательно. Параллельное сопротивление учитывает потери на гистерезис и вихревые токи в магнитном сердечнике. Это параллельное сопротивление зависит от материала сердечника, рабочей частоты и магнитного потока в сердечнике.

Паразитная емкость появляется в связи с тем, что витки катушки находятся близко друг к другу. Любые два витка провода можно рассмотреть как две обкладки маленького конденсатора. Витки разделяются изолятором, таким как воздух, изоляционный лак, лента или иной изоляционный материал. Относительная диэлектрическая проницаемость материалов, используемых для изоляции, увеличивает емкость обмотки. Чем выше эта проницаемость, тем выше емкость. В некоторых случаях дополнительная емкость может появиться также между катушкой и противовесом, если катушка расположена над ним. На высоких частотах реактивное сопротивление паразитной емкости может быть весьма высоким и игнорировать его нельзя. Для уменьшения паразитной емкости используются различные методы намотки катушек.

Для уменьшения паразитной емкости катушки с высокой добротностью для радиопередатчиков наматывают так, чтобы было достаточно большое расстояние между витками

Если индуктивность большая, то сопротивление обмотки (R_w на схеме) игнорировать уже нельзя. Тем не менее, оно мало по сравнению с реактивным сопротивлением больших катушке на высоких частотах. Однако, на низких частотах и на постоянном токе это сопротивление необходимо учитывать, так как в этих условиях через катушку могут протекать значительные токи.

Катушки индуктивности и обмотки в различных устройствах

Плагин Ferrite: Расчет индуктивности на ферритовом стержне

В отличии от тороидальной индуктивности на ферритовом кольце, магнитный поток катушки на ферритовом стержне не замкнут целиком внутри феррита и каждая силовая линия проходит и по ферритовому стержню и по воздуху, поэтому расчет такой катушки представляет довольно сложную задачу. Индуктивность зависит от:

• магнитной проницаемости ферритового стержня и его размеров;
• размеров самой катушки;
• взаимного соотношения размеров катушки и стержня;
• положения катушки относительно центра стержня.

Расчет индуктивности катушки на ферритовом стержне основан на определении относительной эффективной проницаемости стержня. Другими словами, нам нужно определить насколько возрастет индуктивность катушки с «воздушным сердечником» если внутрь нее вставить ферритовый стержень. Основная формула выглядит вот так:

,где L_f / L_air — отношение индуктивности катушки с ферритом к индуктивности той же катушки без феррита, а коэффициенты x, k и μ_fe вычисляются по следующему алгоритму:

1. l’ = l_c + 0.45 d_c;
2. φ_φmax ≈ 1 / [ 1 + { ( ( l_f — l_c ) / d_f )1.4 } / ( 5 μ ) ];
3. C_anf = 0.5 π ε ( l_f — l_c ) / [ ln { 2 ( l_f + d_f) / d_f } — 1 ];
4. k = [ (φ_φmax C_anf / ε ) + 2 d_f ] / 2 d_c
5. x = 5.1 [ l’ / d_c ] / [1+ 2.8 ( d_c / l’ )];
6. μ_fe = ( μ -1) ( d_f /d_c)2 +1;

где ε = 8,8542*10-12 Ф/м — электрическая постоянная, μ — начальная магнитная проницаемость материала стержня. Основные размеры в метрах, обозначения понятны из рисунка:

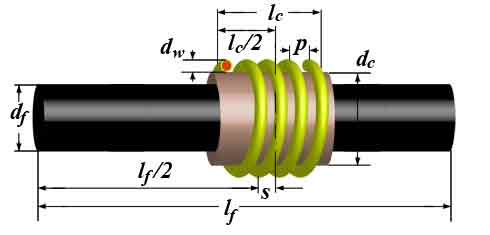
Немного теории обосновывающей этот алгоритм.

• Можно считать что воздушная катушка имеет магнитную цепь состоящую из двух частей. Снаружи катушки и внутри нее. Они отличаются плотностью силовых линий и . Если магнитное сопротивление внутренней части магнитной цепи выше, чем наружной части (а это так, поскольку ее площадь поперечного сечения намного меньше), тогда применение феррита уменьшает это сопротивление и имеет эффект увеличения индуктивности. Это отношение двух частей магнитных сопротивлений магнитной цепи воздушной катушки обозначено в основной формуле как x и вычисляется на 5-ом шагу алгоритма.
• Параметр μ_fe учитывает случай, когда обмотка не плотно прилегает к стержню, т.е. между стержнем и обмоткой существует радиальный зазор.
• Параметр C_anf учитывает влияние частей стержня, которые выступают за пределы катушки. Эти части уменьшают магнитное сопротивление внешней части магнитной цепи и также увеличивают индуктивность.
• Параметр φ_φmax учитывает конечное магнитное сопротивление феррита. Этот параметр, наряду с параметром C_anf используется для расчета коэффициента k из основного уравнения

При смещении катушки относительно стержня индуктивность катушки уменьшается, это обстоятельство учитывается с помощью поправочного коэффициента K:

,где

sh — относительное смещение = смещение s деленное на половину длины сердечника [sh = s / ( lf / 2 )].

Эта формула получена методом регрессионного анализа и справедлива при s = 0,05 — 0,75

В итоге индуктивность катушки на ферритовом стержне определяется по следующей формуле:

Индуктивность катушки  «воздушным» сердечником L_air рассчитывается по алгоритму расчета однослойной катушки с учетом шага намотки. Длину намотки можно определить по следующей формуле:

,где

• N — число витков.
• d_w — диаметр провода.
• p — шаг намотки.

Алгоритм имеет следующие ограничения в расчетах:

• шаг намотки не может превышать удвоенного диаметра провода;
• диаметр катушки не может быть больше удвоенного диаметра стержня;
• длина намотки должна быть меньше 3/4 длины стержня;
• длина стержня должна быть не менее чем в 12 раз больше его диаметра;
• при смещении катушки она не должна доходить до края стержня на 1/8 его длины;
• начальная магнитная проницаемость стержня должна быть больше 100;

Также как и в дросселе на ферритовом кольце с немагнитным зазором, при больших значениях начальной магнитной проницаемости стержня его эффективная магнитная проницаемость слабо зависит от начальной и составляет величину не более нескольких десятков.

Кроме того, вы можете воспользоваться онлайн-калькулятором катушки на ферритовом стержне.

Особая благодарность за конструктивную помощь и соавторство в разработке методики расчета.

Особенности расчёта катушек индуктивности

Кроме конструктивных параметров, на индуктивность влияет также параметры обмоточного провода (диаметр, толщина изоляции, шаг намотки), хотя в большинстве случаев влияние их незначительно, но в некоторых случаях, например, при большом шаге намотки их следует учитывать. Поэтому общая индуктивность катушки можно представить следующим выражением

где L_Р – расчётная индуктивность;

∆L – поправка на «изоляцию», ∆L = ∆₁L + ∆₂L;

∆₁L – поправка учитывающая влияние индуктивности витков;

∆₂L – поправка учитывающая влияние взаимной индуктивности витков.

В большинстве случаев, например, при плотной намотке «виток к витку» поправка ∆L составляет несколько процентов от расчётной индуктивности L_Р, поэтому если нет необходимости в точном значении общей индуктивности L, поправку на изоляцию ∆L можно не учитывать.

Особенности расчёта круговых катушек индуктивности состоят в следующем:

1. При определении расчётной индуктивности L_P, средний диаметр принимается равным среднему диаметру реальной катушки;

2. Длина намотки l и толщина намотки t принимается равными шагу обмотки (p – шаг по длине катушки, q – шаг по толщине намотки) умноженному на количество слоёв ω в том или ином направлении

3. Если у катушки в каком-либо направлении (по длине намотки l или по толщине намотки t) имеется только один ряд (или слой), то в этом направлении размер l или t можно принять равным нулю, то есть расчёт ведётся как для соленоида или плоской катушки.

4. В некоторых случаях, при большом диаметре провода или шаге намотки у однослойных катушках размер l или t принимается равным диаметру голого провода d.

5. Так как величина поправки на взаимную индуктивность ∆₂L в несколько раз меньше, чем поправка на индуктивность витков ∆₁L, то при расчётах можно учитывать только ∆₁L.

Приступим к расчётным выражениям, в начале рассчитаем простейшие круговые катушки – соленоид и плоскую катушку.

Факторы, влияющие на индуктивность катушки

На индуктивность катушки влияют несколько факторов.

• Количество витков. Катушка с большим количеством витков имеет бóльшую индуктивность по сравнению с катушкой с меньшим количеством витков.
• Длина намотки. Две катушки с одинаковым количеством витков, но разной длиной намотки имеют разную индуктивность. Более длинная катушка имеет меньшую индуктивность. Это связано с тем, что магнитное поле менее компактной катушки более слабое и оно не может хорошо концентрироваться в растянутой катушке.
• Диаметр катушки. Две плотно намотанные катушки с одинаковым количеством витков и разными диаметрами имеют разную индуктивность. Катушка с бóльшим диаметром имеет бóльшую индуктивность.
• Сердечник. Для увеличения индуктивности в катушку часто вставляется сердечник из материала с высокой магнитной проницаемостью. Сердечники с более высокой магнитной проницаемостью позволяют получить более высокую индуктивность. Сердечники, изготовленные из магнитной керамики — феррита, часто используются в катушках и трансформаторах различных электронных устройств, так как у них очень низкие потери на вихревые токи.

Упрощенная эквивалентная схема реальной катушки индуктивности: R_w — сопротивление обмотки и ее выводов; L — индуктивность идеальной катушки; R_l — сопротивление вследствие потерь в сердечнике; и C_w — паразитная емкость катушки и ее выводов.