Закон кулона

Закон Кулона и квантовая электродинамика

С точки зрения квантовой электродинамики взаимодействие заряженных тел происходит посредством обмена виртуальными фотонами. Существование таких ненаблюдаемых частиц и нулевой массы, но не нулевыго заряда косвенно подтверждается принципом неопределенности. Согласно этому принципу, виртуальный фотон может существовать между мгновениями испускания такой частицы и ее поглощения. Чем меньше расстояние между телами, тем меньше времени затрачивает фотон на прохождение пути, следовательно, тем больше энергия испускаемых фотонов. При небольшой дистанции между наблюдаемыми зарядами принцип неопределенности допускает обмен и коротковолновыми и длинноволновыми частицами, а при больших расстояниях коротковолновые фотоны в обмене не участвуют.

Задача 2

Два одинаковых заряженных шарика подвешены в среде с диэлектрической проницаемостью на нитях одинаковой длины , закрепленных в одной точке. Определите модуль заряда шариков, если нити находятся под прямым углом друг к другу (см. рис. 15). Размеры шариков пренебрежимо малы по сравнению с расстоянием между ними. Массы шариков равны .

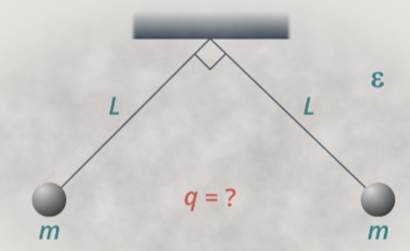
Рис. 15. Рисунок к условию задачи 2

Порассуждаем: на каждый из шариков будут действовать три силы – сила тяжести ; сила электростатического взаимодействия и сила натяжения нити (см. рис. 16).

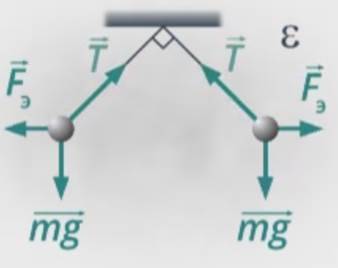
Рис. 16. Силы, действующие на шарики

По условию шарики одинаковые, то есть их заряды равны как по модулю, так и по знаку, а значит, сила электростатического взаимодействия в данном случае будет силой отталкивания (на рис. 16 силы электростатического взаимодействия направлены в разные стороны). Так как система находится в равновесии, будем использовать первый закон Ньютона:

Так как в условии сказано, что шарики подвешены в среде с диэлектрической проницаемостью , а размеры шариков пренебрежимо малы по сравнению с расстоянием между ними, то в соответствии с законом Кулона сила, с которой будут отталкиваться шарики, будет равна:

Решение

Распишем первый закон Ньютона в проекциях на оси координат. Ось направим горизонтально, а ось вертикально (см. рис. 17).

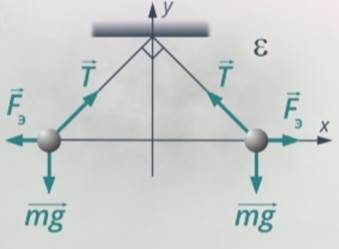
Рис. 17. Выбор направления осей координат

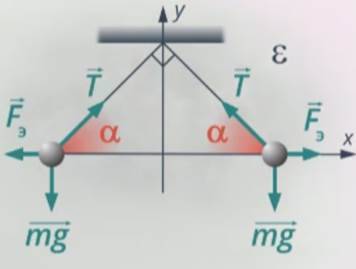
Рис. 18. Силы в проекциях на оси координат

Так как на шарики действуют одинаковые силы тяжести и силы электростатического взаимодействия, нити тоже одинаковые – они отклонятся на одинаковые углы (см. рис. 19).

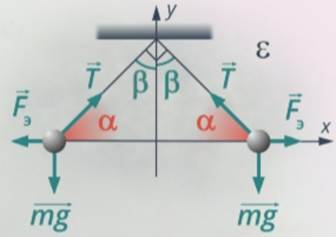
Рис. 19. Углы, на которые отклоняются шарики, одинаковые

В сумме эти углы дают нам , это означает, что:

Тогда из прямоугольного треугольника можно найти углом :

Добавим к двум уравнениям, которые мы записали, выражение для модуля силы электростатического взаимодействия:

Расстояние найдем геометрически – найдем прилежащий к углу катет и умножим его на 2:

Мы получили систему из 4-х уравнений:

Математическое решение можно пронаблюдать в свертке.

Ответ:

Решение системы уравнений

Выразим из второго уравнения силу натяжения нити и подставим в первое:

Отсюда выразим силу электростатического взаимодействия:

Приравняем выражение для силы электростатического взаимодействия, которое мы сейчас выразили с третьим уравнением:

Подставим сюда выражение для

Выразим искомый заряд

Так как угол , то , тогда:

На этом наш урок закончен

Спасибо за внимание

Список литературы

1. Соколович Ю.А., Богданова Г.С Физика: Справочник с примерами решения задач. – 2-е издание передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.

2. Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика: Учеб. для общеобразоват. учреждений. Базовый и профильный уровни. 19-е издание – М.: Просвещение, 2010.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-сайт physics.ru ()

2. Интернет-сайт «Класс!ная физика» (Источник)

Домашнее задание

1. Запишите формулу закона Кулона.

2. Как взаимодействуют разноименно заряженные тела?

3. Решите задачу: два заряда, 10 нКл и -2 нКл, закреплены на расстоянии 10 см друг от друга. Определите силу, с которой они взаимодействуют.

2. История открытия

Догадки о том, что взаимодействие между електризованимы телами подчиняется тому же закону оберененои пропорциональности квадрату расстояния, и тяжести, неоднократно высказывались исследователями в середине 18 в. В начале 1770-х ее экспериментально открыл Генри Кавендиш, однако своих результатов не опубликовал, и о них стало известно только в конце 19 в. после изучения и публикации его архивов. Шарль Кулон опубликовал закон 1785 году в двух мемуарах, представленных на рассмотрение Французской академии наук . 1835 Карл Гаусс опубликовал выведенную на основе закона Кулона, теорему Гаусса. В виде теоремы Гаусса закон Кулона входит в основных уравнений электродинамики.

Применение на практике

Работы Кулона очень важны в электростатике, на практике они применяется в целом ряде изобретений и устройств. Ярким примером можно выделить молниеотвод. С его помощью защищают здания и электроустановки от грозы, предотвращая тем самым пожар и выход из строя оборудования. Когда идёт дождь с грозой на земле появляется индуцированный заряд большой величины, они притягиваются в сторону облака. Получается так, что на поверхности земли появляется большое электрическое поле. Возле острия молниеотвода оно имеет большую величину, в результате этого от острия зажигается коронный разряд (от земли, через молниеотвод к облаку). Заряд от земли притягивается к противоположному заряду облака, согласно закону Кулона. Воздух ионизируется, а напряженность электрического поля уменьшается вблизи конца молниеотвода. Таким образом, заряды не накапливаются на здании, в таком случае вероятность удара молнии мала. Если же удар в здание и произойдет, то через молниеотвод вся энергия уйдет в землю.

В серьезных научных исследованиях применяют величайшее сооружение 21 века – ускоритель частиц. В нём электрическое поле выполняет работу по увеличению энергии частицы. Рассматривая эти процессы с точки зрения воздействия на точечный заряд группой зарядов, тогда все соотношения закона оказываются справедливыми.

Напоследок рекомендуем просмотреть видео, на котором предоставлено подробное объяснение Закона Кулона:

Полезное по теме:

Закон Джоуля-Ленца
Зависимость сопротивления проводника от температуры
Правила буравчика
Закон Ома простыми словами

Определение электрического поля (Е)

Электрическое поле (напряженность поля) E в данной точке определяется как значение, равное отношению силы F, действующей на положительный испытательный заряд q, к значению нагрузки:

Движение заряженных частиц в поле происходит под действием силы F = Q*E.

Аддитивность полей

Поле E является аддитивным вектором, что означает, что результирующее электрическое поле представляет собой векторную сумму полей E 1 , E 2 , E 3 …, полученных из отдельных зарядов:

Линии напряженности электрических полей

Концепция силовых линий поля была также введена Майклом Фарадеем (1791-1867). Линии напряженности поля представляют собой воображаемые кривые в пространстве, находящиеся в каждой точке, касающейся вектора E в этой точке. Это также означает, что в каждой точке линии поля имеется касательный вектор силы, действующий в этом поле для испытательной нагрузки (небольшой положительный заряд). Как показано на рисунке ниже, силовая линия — это траектория положительного испытательного заряда (маленький красный шарик), движущегося в поле E , причем сила F является результирующей (векторной суммой) двух сил: силы, отталкивающей испытательный заряд от положительного заряда F Q, и силы притяжения испытательная нагрузка на отрицательный заряд F q. Такая картина силовых линий верна только тогда, когда пренебрегают силами инерции (центробежными), возникающими из-за ненулевой массы груза. Линии напряженности поля никогда не пересекаются друг с другом. Представляя силовые линии, принимается соглашение о вытягивании, согласно которому плотность силовых линий пропорциональна напряженности поля в этом месте. Силовые линии в окрестности системы двух точечных нагрузок, положительной и отрицательной, одинакового абсолютного значения показаны на рисунке:

Один заряд, помещенный в вакуум, окружен радиальной системой силовых линий.

Как направлены силы

Заряды взаимодействуют друг с другом в зависимости от их полярности — одинаковые отталкиваются, а разноименные (противоположные) притягиваются.

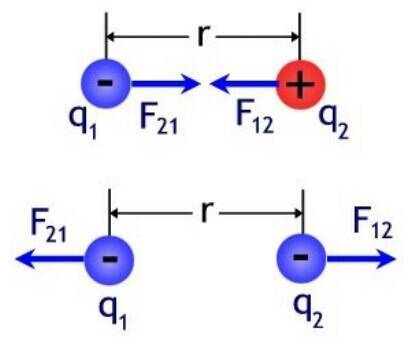
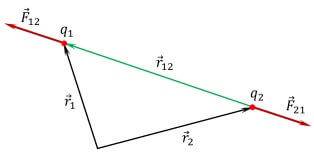
Кстати это главное отличие от подобного закона гравитационного взаимодействия, где тела всегда притягиваются. Силы направлены вдоль линии, проведенной между ними, называют радиус-вектором. В физике обозначают как r₁₂ и как радиус-вектор от первого ко второму заряду и наоборот. Силы направлены от центра заряда к противоположному заряду вдоль этой линии, если заряды противоположны, и в обратную сторону, если они одноименные (два положительных или два отрицательных). В векторном виде:

Сила, приложенная к первому заряду со стороны второго обозначается как F_12.Тогда в векторной форме закон Кулона выглядит следующим образом:

Для определения силы приложенной ко второму заряду используются обозначения F₂₁ и R₂₁.

Если тело имеет сложную форму и оно достаточно большое, что при заданном расстоянии не может считаться точечным, тогда его разбивают на маленькие участки и считают каждый участок как точечный заряд. После геометрического сложения всех получившихся векторов получают результирующую силу. Атомы и молекулы взаимодействуют друг с другом по этому же закону.

Cтепень точности закона Кулона

Закон Кулона — экспериментально установленный факт. Его справедливость неоднократно подтверждалась всё более точными экспериментами. Одним из направлений таких экспериментов является проверка того, отличается ли показатель степени r
в законе от 2. Для поиска этого отличия используется тот факт, что если степень точно равна двум, то поле внутри полости в проводнике отсутствует, какова бы ни была форма полости или проводника.

Эксперименты, проведённые в 1971 г. в США Э. Р. Уильямсом, Д. Е. Фоллером и Г. А. Хиллом, показали, что показатель степени в законе Кулона равен 2 с точностью до .

Для проверки точности закона Кулона на внутриатомных расстояниях У. Ю. Лэмбом и Р. Резерфордом в 1947 г. были использованы измерения относительного расположения уровней энергии водорода. Было установлено, что и на расстояниях порядка атомных 10−8 см, показатель степени в законе Кулона отличается от 2 не более чем на 10−9.

Коэффициент в законе Кулона остается постоянным с точностью до 15·10−6.

Поправки к закону Кулона в квантовой электродинамике

На небольших расстояниях (порядка комптоновской длины волны электрона, ≈3.86·10−13 м, где — масса электрона, — постоянная Планка, — скорость света) становятся существенными нелинейные эффекты квантовой электродинамики: на обмен виртуальными фотонами накладывается генерация виртуальных электрон-позитронных (а также мюон-антимюонных и таон-антитаонных) пар, а также уменьшается влияние экранирования (см. перенормировка). Оба эффекта ведут к появлению экспоненциально убывающих членов порядка в выражении для потенциальной энергии взаимодействия зарядов и, как результат, к увеличению силы взаимодействия по сравнению с вычисляемой по закону Кулона. Например, выражение для потенциала точечного заряда в системе СГС, с учётом радиационных поправок первого порядка принимает вид:

где — комптоновская длина волны электрона, — постоянная тонкой структуры и . На расстояниях порядка ~ 10−18 м, где — масса W-бозона, в игру вступают уже электрослабые эффекты.

В сильных внешних электромагнитных полях, составляющих заметную долю от поля пробоя вакуума (порядка ~1018 В/м или ~109 Тл, такие поля наблюдаются, например, вблизи некоторых типов нейтронных звёзд, а именно магнитаров) закон Кулона также нарушается в силу дельбрюковского рассеяния обменных фотонов на фотонах внешнего поля и других, более сложных нелинейных эффектов. Это явление уменьшает кулоновскую силу не только в микро- но и в макромасштабах, в частности, в сильном магнитном поле кулоновский потенциал падает не обратно пропорционально расстоянию, а экспоненциально.

Закон Кулона и поляризация вакуума

Явление поляризации вакуума в квантовой электродинамике заключается в образовании виртуальных электронно-позитронных пар. Облако электронно-позитронных пар экранирует электрический заряд электрона. Экранировка растет с ростом расстояния от электрона, в результате эффективный электрический заряд электрона является убывающей функцией расстояния . Эффективный потенциал, создаваемый электроном с электрическим зарядом , можно описать зависимостью вида . Эффективный заряд зависит от расстояния по логарифмическому закону:

— т. н. постоянная тонкой структуры ≈7.3·10−3;

— т. н. классический радиус электрона ≈2.8·10−13 см.

Эффект Юлинга

Явление отклонения электростатического потенциала точечных зарядов в вакууме от значения закона Кулона известно как эффект Юлинга, который впервые вычислил отклонения от закона Кулона для атома водорода. Эффект Юлинга даёт поправку к лэмбовскому сдвигу 27 мггц.

В сильном электромагнитном поле вблизи сверхтяжелых ядер с зарядом 170″ src=»http://upload.wikimedia.org/math/0/d/7/0d7b5476a5437d2a99326cf04b131458.png»> осуществляется перестройка вакуума, аналогичная обычному фазовому переходу. Это приводит к поправкам к закону Кулона.

Все формулы

Между электрическими зарядами действует сила. Как она зависит от величины зарядов и других факторов?Этот вопрос исследовал в 1780-е годы французский физик Шарль Кулон (1736-1806).

Он воспользовался крутильными весами, очень похожими на те, которые применял Кавендиш для определения гравитационной постоянной.Если к шарику на конце стержня, подвешенного на нити, подности заряд, стержень слегка отклоняется, нить закручивается, и угол поворота нити будет пропорционален действующей между зарядами силе (крутильные весы).

С помощью этого прибора Кулон определил зависимость силы от величины зарядов и расстояния между ними. В те времена еще не было приборов для точного определения величины заряда, но Кулон сумел приготовить небольшие шарики с известным соотношением зарядов.

Задача 1

В вершинах правильного шестиугольника со стороной помещены друг за другом заряды . Найдите силу, действующую на заряд , расположенный в центре шестиугольника (см. рис. 6).

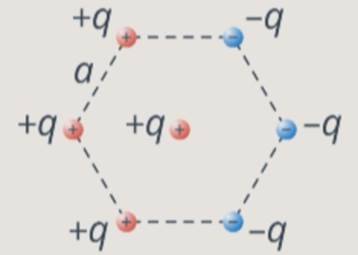
Рис. 6. Рисунок к условию задачи 1

Порассуждаем: заряд, находящийся в центре шестиугольника, будет взаимодействовать с каждым из зарядов, находящихся в вершинах шестиугольника. В зависимости от знаков это будет сила притяжения или сила отталкивания. С зарядами 1, 2 и 3, которые являются положительными, заряд, находящийся в центре, будет испытывать электростатическое отталкивание (см. рис. 7).

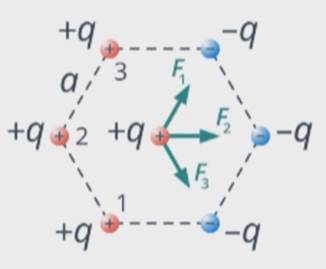
Рис. 7. Электростатическое отталкивание

А с зарядами 4, 5 и 6 (отрицательными) заряд в центре будет иметь электростатическое притяжение (см. рис. 8).

Рис. 8. Электростатическое притяжение

Суммарная сила, действующая на заряд, находящийся в центре шестиугольника, будет равнодействующей сил ,,,, и, модуль каждой из которых можно найти с помощью закона Кулона. Приступим к решению задачи.

Решение

Силы взаимодействия заряда, который находится в центре, с каждым из зарядов в вершинах зависит от модулей самих зарядов и расстояния между ними. Расстояние от вершин к центру правильного шестиугольника одинаковое, модули у взаимодействующих зарядов в нашем случае тоже равны (см. рис. 9).

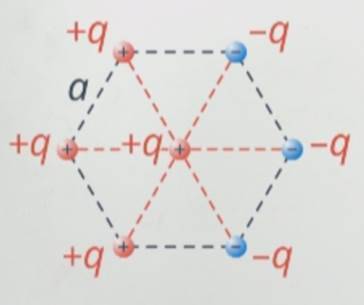
Рис. 9. Расстояния от вершин до центра в правильном шестиугольнике равны

А значит, все силы взаимодействия заряда в центре шестиугольника с зарядами в вершинах будут равны по модулю. Воспользовавшись законом Кулона, мы можем найти этот модуль:

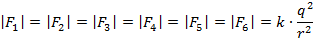
Расстояние от центра до вершины в правильном шестиугольнике равно длине стороны правильного шестиугольника, которая нам известна из условия, поэтому:

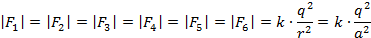
Теперь нам необходимо найти векторную сумму – для этого выберем систему координат: ось вдоль силы , а ось перпендикулярно (см. рис. 10).

Рис. 10. Выбор осей

Найдем суммарные проекции на оси – модуль каждой из них обозначим просто .

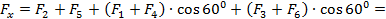
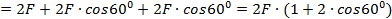
Так как силы и сонаправлены с осью , а находятся под углом к оси (см. рис. 11).

Рис. 11. Направление сил относительно оси

Проделаем такие же действия для оси :

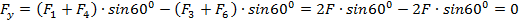
Знак «-» – потому что силы и направлены в противоположную сторону оси . То есть проекция суммарной силы на ось , которую мы выбрали, будет равна 0. Получается, что суммарная сила будет действовать только вдоль оси , остается подставить сюда только выражения для модуля сил взаимодействия и и получить ответ. Суммарная сила будет равна:

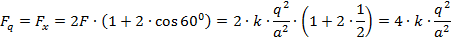
Задача решена.

Примечания

Сивухин Д. В. Общий курс физики. — М.: Физматлит; Изд-во МФТИ, 2004. — Т. III. Электричество. — С. 17. — 656 с. — ISBN 5-9221-0227-3.
Ландау Л. Д., Лифшиц Е. М. Теория поля. — Издание 8-е, стереотипное. — М.: Физматлит, . — С. 132. — («Теоретическая физика», том II). — ISBN 5-9221-0056-4.
Ландсберг Г. С. Элементарный учебник физики. Том II. Электричество и магнетизм. — М.: Наука, 1964. — Тираж 100 000 экз. — С. 33.
Ландау, Л. Д., Лифшиц, Е. М. Квантовая механика (нерелятивистская теория). — М., 2002. — С. 74. — («Теоретическая физика», том III).
Бете Х. Квантовая механика. — Пер. с англ., под ред. В. Л. Бонч-Бруевича. — М.: Мир, 1965. — С. 11.
Пайерлс Р. Е. Законы природы. пер. с англ. под ред. проф. Халатникова И. М. , Государственное издательство физико-математической литературы, М., 1959, тир. 20000 экз., 339 с., Гл. 9 «Электроны при высоких скоростях», п. «Силы при больших скоростях. Другие трудности», c. 263
Novi Comm. Acad. Sc. Imp. Petropolitanae, v. IV, 1758, p. 301.
J. Priestley. The History and present state of Electricity with original experiments. London, 1767, p. 732.
Уиттекер Э. История теории эфира и электричества. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 76. — 512 с. — ISBN 5-93972-070-6.
‘Филонович С. Р. Кавендиш, Кулон и электростатика. — М: Знание, 1988. — С. 48.
Р. Фейнман, Р. Лейтон, М. Сэндс, Фейнмановские лекции по физике, вып. 5, «Электричество и магнетизм», пер. с англ., под ред. Я. А. Смородинского, изд. 3, М., Едиториал УРСС, 2004, ISBN 5-354-00703-8 (Электричество и магнетизм), ISBN 5-354-00698-8 (Полное произведение), гл. 4 «Электростатика», п. 1 «Статика», с. 70-71;
Р. Фейнман, Р. Лейтон, М. Сэндс, Фейнмановские лекции по физике, вып. 5, «Электричество и магнетизм», пер. с англ., под ред. Я. А. Смородинского, изд. 3, М., Едиториал УРСС, 2004, ISBN 5-354-00703-8 (Электричество и магнетизм), ISBN 5-354-00698-8 (Полное произведение), гл. 5 «Применения закона Гаусса», п. 10 «Поле внутри полости проводника», с. 106—108;
Калашников С. Г.,
Электричество, М., ГИТТЛ, 1956, гл. III «Разность потенциалов», п. 34 «Точная проверка закона Кулона», с. 68—69; «Добавления», 1. «Теория опытов Кавендиша и Максвелла», с. 642—645;
E. R. Williams, J. E. Faller, H. A. Hill «New Experimental Test of Coulomb’s Law: A Laboratory Upper Limit on the Photon Rest Mass», Phys. Rev. Lett. 26, 721—724 (1971);
W. E. Lamb, R. C. Retherford. Fine Structure of the Hydrogen Atom by a Microwave Method (англ.) // Physical Review. — Т. 72, № 3. — С. 241—243.
↑ Р. Фейнман, Р. Лейтон, М. Сэндс, Фейнмановские лекции по физике, вып. 5, «Электричество и магнетизм», пер. с англ., под ред. Я. А. Смородинского, изд. 3, М., Едиториал УРСС, 2004, ISBN 5-354-00703-8 (Электричество и магнетизм), ISBN 5-354-00698-8 (Полное произведение), гл. 5 «Применения закона Гаусса», п. 8 «Точен ли закон Кулона?», с. 103;
Берестецкий В. Б., Лифшиц Е. М., Питаевский Л. П. Квантовая электродинамика. — Издание 3-е, исправленное. — М.: Наука, 1989. — С. 565—567. — 720 с. — («Теоретическая физика», том IV). — ISBN 5-02-014422-3.
Окунь Л. Б. Физика элементарных частиц. Изд. 3-е, М.: «Едиториал УРСС», 2005, ISBN 5-354-01085-3, ББК 22.382 22.315 22.3о, гл. 2 «Гравитация. Электродинамика», «Поляризация вакуума», с. 26-27;
«Физика микромира», гл. ред. Д. В. Ширков, М., «Советская энциклопедия», 1980, 528 с., илл., 530.1(03), Ф50, ст. «Эффективный заряд», авт. ст. Д. В. Ширков, стр. 496;
Яворский Б. М. «Справочник по физике для инженеров и студентов вузов» / Б. М. Яворский, А. А. Детлаф, А. К. Лебедев, 8-e изд., перераб. и испр., М.: ООО «Издательство Оникс», ООО «Издательство Мир и образование», 2006, 1056 стр.: илл., ISBN 5-488-00330-4 (ООО «Издательство Оникс»), ISBN 5-94666-260-0 (ООО «Издательство Мир и образование»), ISBN 985-13-5975-0 (ООО «Харвест»), УДК 530(035) ББК 22.3, Я22, «Приложения», «Фундаментальные физические постоянные», с. 1008;
Uehling E. A ., Phys. Rev., 48, 55, (1935)
Швебер С., Бете Г., Гофман Ф. Мезоны и поля. Том 1 Поля гл. 5 Свойства уравнения Дирака п. 2. Состояния с отрицательной энергией c. 56, гл. 21 Перенормировка, п. 5 Поляризация вакуума с 336
Мигдал А. Б. Поляризация вакуума в сильных полях и пионная конденсация// Успехи физических наук Т. 123— в. 3.— 1977 г., ноябрь.— с. 369—403;
Спиридонов О. П. Универсальные физические постоянные.— М.: Просвещение.— 1984.— с. 52-53;

Есть ли пределы применения закона Кулона

Закон Кулона полностью объясняет поведение двух точечных зарядов в вакууме

Но когда речь идет о реальных телах, следует принимать во внимание объемные размеры заряженных тел и характеристики среды, в которой ведется наблюдение. Например, некоторые исследователи наблюдали, что тело, несущее в себе небольшой заряд и принудительно внесенное в электрическое поле другого объекта с большим зарядом, начинает притягиваться к этому заряду

В этом случае утверждение, что одноименно заряженные тела отталкиваются, дает сбой, и следует искать другое объяснение наблюдаемому явлению. Скорее всего, здесь не идет речь о нарушении закона Кулона или принципа сохранения электрического заряда – возможно, что мы наблюдаем неизученные до конца явления, объяснить которые наука сможет немного позже.

Опыт Кулона

Необходимость проведения экспериментов Кулона была вызвана тем, что в середине XVIII в. накопилось много качественных данных об электрических явлениях. Возникла потребность дать им количественную интерпретацию. Поскольку силы электрического взаимодействия были относительно невелики, возникла серьезная проблема в создании метода, который позволил бы произвести замеры и получить необходимый количественный материал.

Французский инженер и ученый Шарль Кулон предложил метод измерения малых сил, который основывался на следующем экспериментальном факте, обнаруженном самим ученым: сила, возникающая при упругой деформации металлической проволоки, прямо пропорциональна углу закручивания, четвертой степени диаметра проволоки и обратно пропорциональна ее длине:

где d – диаметр, l – длина проволоки, φ – угол закручивания. В приведенном математическом выражении коэффициент пропорциональности k находился опытным путем и зависел от природы материала, из которого изготавливалась проволока.

Данная закономерность была использована в так называемых крутильных весах. Созданные весы позволили измерить ничтожно малые силы порядка 5·10-8 Н.

Рис. 3

Крутильные весы (рис. 3, а) состояли из легкого стеклянного коромысла 9 длиной 10,83 см, подвешенного на серебряной проволоке 5 длиной около 75 см, диаметром 0,22 см. На одном конце коромысла располагался позолоченный бузиновый шарик 8, а на другом – противовес 6 – бумажный кружок, смоченный в скипидаре. Верхний конец проволоки прикреплялся к головке прибора 1. Здесь же имелся указатель 2, с помощью которого отсчитывался угол закручивания нити по круговой шкале 3. Шкала была проградуирована. Вся эта система размещалась в стеклянных цилиндрах 4 и 11. В верхней крышке нижнего цилиндра имелось отверстие, в которое вставлялась стеклянная палочка с шариком 7 на конце. В опытах применялись шарики с диаметрами в пределах 0,45 – 0,68 см.

Перед началом эксперимента указатель головки устанавливался на нулевой отметке. Затем шарик 7 заряжался от предварительно наэлектризованного шарика 12. При соприкосновении шарика 7 с подвижным шариком 8 происходило перераспределение заряда. Однако из-за того, что диаметры шариков были одинаковыми, одинаковыми были и заряды на шариках 7 и 8.

Вследствие электростатического отталкивания шариков (рис. 3, б) коромысло 9 поворачивалось на некоторый угол γ (по шкале 10). С помощью головки 1 это коромысло возвращалось в исходное положение. По шкале 3 указатель 2 позволял определять угол α закручивания нити. Общий угол закручивания нити φ = γ + α. Сила же взаимодействия шариков была пропорциональна φ, то есть по углу закручивания можно судить о величине этой силы.

При неизменном расстоянии между шариками (оно фиксировалось по шкале 10 в градусной мере) исследовалась зависимость силы электрического взаимодействия точечных тел от величины заряда на них.

Для определения зависимости силы от заряда шариков Кулон нашел простой и остроумный способ изменения заряда одного из шариков. Для этого он соединял заряженный шарик (шарики 7 или 8) с таким же по размерам незаряженным (шарик 12 на изолирующей ручке). Заряд при этом распределялся поровну между шариками, что и уменьшало исследуемый заряд в 2, 4 и т. д. раз. Новое значение силы при новом значении заряда опять определялось экспериментально. При этом выяснилось, что сила прямо пропорциональна произведению зарядов шариков:

Зависимость силы электрического взаимодействия от расстояния была обнаружена следующим образом. После сообщения шарикам заряда (он был у них одинаковый) коромысло отклонялось на некоторый угол γ. Затем поворотом головки 1 уменьшался этот угол до γ₁. Общий угол закручивания φ₁ = α₁ + (γ — γ₁)(α₁ – угол поворота головки). При уменьшении углового расстояния шариков до γ₂ общий угол закручивания φ₂ = α₂ + (γ — γ₂) . Было замечено, что, если γ₁ = 2γ₂, ТО φ₂ = 4φ₁, т. е. при уменьшении расстояния в 2 раза сила взаимодействия возрастала в 4 раза. Во столько же раз увеличился момент силы, так как при деформации кручения момент силы прямо пропорционален углу закручивания, а значит, и сила (плечо силы оставалось неизменным). Отсюда вытекает вывод: сила взаимодействия двух заряженных шариков обратно пропорциональна квадрату расстояния между ними:

Дата: 29.04.2015

Литература

1. Мякишев Г.Я. Физика: Электродинамика. 10-11 кл.: учеб. для углубленного изучения физики / Г.Я. Мякишев, А.З. Синяков, Б.А. Слободсков. – М.: Дрофа, 2005. – 476 с.

2. Вольштейн С. Л. и др. Методы физической науки в школе: Пособие для учителя / С.Л. Вольштейн, С.В. Позойский, В.В. Усанов; Под ред. С.Л. Вольштейна. – Мн.: Нар. асвета, 1988. – 144 с.