Сложение и вычитание векторов
На рисунке 12, а изображены три вектора A, B и C. На рисунке 12, б показано их сложение по правилу параллелограмма, а именно: сначала найдена сумма двух векторов A и B (B и C, A и C), а затем к ней прибавлен вектор C (A, B). Рисунок 12, в показывает другой способ сложения этих же векторов в четырех вариантах
Обратите внимание на направление вектора суммы. Сравнивая рисунки 12, б и в, легко видеть, что в любом случае получены одинаковые результаты
Рисунок 12. Сложение и вычитание векторов
Для вычитания одного вектора из другого вычитаемый вектор поворачивают на 180° (то есть ему дают обратный знак), после чего по правилу параллелограмма производят сложение (рисунок 12, г). Другой способ вычитания этих же векторов иллюстрирует рисунок 12, д. Заметьте: вектор-разность направлен к концу того вектора, из которого сделано вычитание. Так, на рисунке 12, д, слева, вектор-разность направлен к концу вектора B.
Техника построения векторов
Техника построения векторов для двух э. д. с. поясняется рисунком 10, а. Слева на нем изображены синусоиды и ясно видно, что э. д. с. e2 опережает e1 на угол α. Справа э. д. с. e1 изображена вектором E1М, который расположен горизонтально (то есть так, чтобы его проекция на ось 1–1 была равна мгновенному значению e1 в точке ) и стрелкой показано направление вращения 1. Затем по этому направлению отложен угол α и построен вектор э. д. с. E2М.
Рисунок 10. Определение сдвига фаз при помощи вектора
Построение можно выполнить иначе. После построения вектора E1М (который расположен горизонтально) через точку пересечения синусоиды e2 с вертикалью 2–2 проведена горизонтальная штриховая линия (она отсекает мгновенное значение э. д. с. e2, соответствующее точке ). Затем радиусом длиной E2М из точки ‘ как из центра сделана засечка, после чего построен вектор E2М. При таком построении угол α получается автоматически.
Примеры векторных диаграмм (то есть совокупности векторов, изображающих синусоидальные величины одинаковой частоты для различных углов сдвига фаз между e1 и e2) даны на рисунке 10, б–е.
Обратите особое внимание на рисунок 10, е, который соответствует рисунку 10, г и показывает, что как бы ни располагалась на чертеже векторная диаграмма, сдвиг фаз от этого на ней не изменяется и это весьма важно
Синусоида
Кривая на рисунке 2 – синусоида показывает, что э. д. с. непрерывно изменяется, причем число ее мгновенных значений в течении периода безгранично: их столько же, сколько точек может поместится на синусоиде. В течение периода мгновенные одинаковые значения э. д. с. одного знака бывают дважды. За период э. д. с. 2 раза достигает наибольших (максимальных, амплитудных) значений, но один раз это положительное, другой раз – отрицательное значение. Одним словом, по синусоиде можно составить самое полное представление об изменениях синусоидальной э. д. с. (тока) с течением времени.
Видео 2. Синусоида
Получение многофазных токов
Если в генераторе имеется одна, а несколько обмоток и если они одинаковы по конструкции, числу витков, сечению провода, то синусоиды, изображающие изменение э. д. с. в каждом из них, одинаковы. Однако располагать их на чертеже нужно в соответствии как со взаимным расположением обмоток, так и с направлением вращения. Поясним на примерах.
Рисунок 4. Расположение синусоид на чертежах в зависимости от направления вращения ротора генератора
На рисунке 4 показан генератор с двумя обмотками ax и by, которые размещены в одних и тех же пазах и, следовательно, одинаково перемещаются относительно магнита. Поэтому синусоиды, изображающие изменение э. д. с. в обеих обмотках, совпадают. Но если вращение происходит против часовой стрелки, наблюдение за изменениями э. д. с. начинается в тот момент, когда обмотки занимают положение, показанное на чертеже, и синусоиды начерчены, как на рисунке 4, а, то при вращении по часовой стрелке синусоиды изображают иначе (рисунок 4, б). Почему? Потому, что в первом случае проводники раньше проходят под северным полюсом, во втором – раньше под южным.
Рисунок 5. Сдвиг э. д. с. двух обмоток на четверть периода
Генератор на рисунке 5, а тоже имеет две обмотки, но расположенные под прямым углом. Поэтому они проходят под полюсами неодновременно. Значит, максимальные значения э. д. с. в них наступают в разное время и, следовательно, синусоиды должны быть сдвинуты. Остается выяснить, на какую часть периода и в какую сторону. Решают эти вопросы следующим образом.
1. Синусоиду э. д. с. одной обмотки, например ax, располагают на чертеже произвольно и через точку , от которой в дальнейшем будет вестись отсчет времени, проводят вертикаль 1–1 (рисунок 5, б). 2. Определяют по рисунку 5, а, какому положению проводника соответствует точка и где в это время находится проводник b: опережает он проводник a по направлению вращения или отстает от него. В нашем случае проводник b опережает проводник a. Действительно, последний еще на нейтрали, э. д. с. в нем равна нулю, а проводник b – уже под полюсом и его э. д. с. достигла максимума. 3. Определяют, какой знак имеет э. д. с. в обмотке by в точке , чтобы знать, как начинать построение синусоиды э. д. с. обмотки by в точке – под горизонтальной осью или на ней. Если обмотка by находится в области того же полюса, к которому при вращении приближается обмотка ax, значит знаки у э. д. с. одинаковы. В нашем примере э. д. с. обмотки ax положительна и обе обмотки находятся в области одного и того же полюса. Поэтому синусоида э. д. с. обмотки by в точке тоже должна быть положительна. 4. Определяют на какую часть периода обмотка by сдвинута относительно обмотки ax. Это видно из рисунка 5, а и г, на которых представлены соответственно двухполюсный и четырехполюсный генераторы. Длительность периода Т в любом случае определяется расстоянием между одноименными полюсами и частотой (скоростью) вращения. Нетрудно видеть, что расстояние между началами обмоток, то есть между проводниками a и b, равно четверти периода. 5. Остается совместить синусоиды э. д. с. Обмоток ax и by, что сделано на рисунке 5, д, где ясно виден сдвиг между ними на четверть периода Т/4, или на 90 электрических градусов.
Генератор с тремя обмотками ax, by и cz показан на рисунке 6. Обмотки равномерно распределены по окружности, то есть сдвинуты друг относительно друга на треть периода Т/3 или на 120 эл. градусов. При данном расположении обмоток и вращении против часовой стрелки э. д. с. обмотки ax опережает на Т/3 э. д. с. обмотки by, которая в свою очередь опережает на Т/3 э. д. с. обмотки cz.
Рисунок 6. Электродвижущие силы трех обмоток, сдвинутых на треть периода
Каждая обмотка генератора (трансформатора, электродвигателя переменного тока) обычно называется фазой.
Генераторы с одной обмоткой являются однофазными, с двумя обмотками – двухфазными, с тремя – трехфазными и так далее. Если э. д. с. в разных обмотках достигают нулевых (или максимальных) значений в разное время, то говорят, что между фазами существует сдвиг, который определяют в долях периода или электрических градусах.
Частотный способ определения скорости вращения
Частотный метод для СТГ является самым точным так как на частоту выходного сигнала не оказывают влияния такие факторы как, изменения температуры, величина зазора между статором и ротором, уменьшение магнитного потока вызванное старением магнитов и т.д..
Но, к сожалению, при определении скорости вращения частотным способом требуется время для определения частоты выходного сигнала Uвых путём накопления импульсов, что не даёт возможности получать мгновенно информацию об изменениях скорости.
После определения частоты Fout выходного сигнала Uвых , скорость вращения ротора вычисляют по формуле:
где Frot — частота вращения ротора в Гц; Fout — частота сигнала Uвых на выходе тахогенератора Гц; p — число пар полюсов ротора тахогенератора.
Для более точного определения частоты вращения ротора необходимо большее количество времени, в течении которого частота может изменяться. А изменение частоты во время накопления импульсов для её определения вносит погрешность в измерения. Это плохо сказывается на динамичности системы управления в целом, т.к. её схема управления, в таких случаях, более медленно компенсирует уменьшение или увеличение скорости вращения. Чтобы как-то уменьшить вышеуказанный недостаток, используют СТГ с большим количеством полюсов. Это даёт возможность сократить время для определения выходной частоты, что в свою очередь позволяет сократить время реакции схемы управления.
Частоту выходного сигнала можно определять по формуле приведенной ниже, но при этом усложняется электрическая схема, что не всегда приемлемо.
где Fout – расчётное значение выходной частоты тахогенератора; N – число накопленных импульсов; Т – длина каждого периода;
Векторы
В технике переменных токов периодические изменения э. д. с. (токов) часто изображают векторами, то есть отрезками прямой определенной длины и определенного направления.
Для определения мгновенных значений вектор должен иметь длину, соответствующую максимальному значению э. д. с. Его начальная фаза совпадает с направлением горизонтальной оси. Затем вектор вращают против часовой стрелки и проектируют на неподвижную вертикальную ось. Длины проекций и определяют мгновенные значения э. д. с. для каждого угла поворота, что иллюстрирует рисунок 9. На рисунке 9 изменения э. д. с. представлены как синусоидой, на которой отмечены мгновенные значения э. д. с. через каждую восьмую часть периода, так и проекциями вектора на ось для тех же долей периода.
Рисунок 9. Определение мгновенных значений э. д. с. при вращении вектора
Фаза
Выше уже указывалось, что обмотки генераторов, трансформаторов и электродвигателей называют фазами. Но слово «фаза» в электротехнике употребляют еще в нескольких значениях.
Фазами также называют провода трехфазных линий в отличие от нулевого провода. Фазы обозначают буквами A, B, C (a, b, c) или Ж, З, К, так как на электростанциях и подстанциях шины, принадлежащие разным фазам окрашивают желтой, зеленой и красной красками. Нуль обозначают цифрой , а иногда буквой N (нейтраль).
Фазой в широком смысле этого слова называется отдельный момент в развитии какого-либо явления. В периодических процессах (к которым относятся и изменения э. д. с. и тока) фазой называется значение величины, характеризующей состояние колебательного процесса в каждый момент времени.
Таким образом, фазой можно назвать и угол поворота обмотки (так как каждому углу соответствует определенное значение э. д. с.) и время, прошедшее от начала периода. Начало периода, когда э. д. с. равна нулю, часто называют нулевой фазой.
Фазовые углы, определяющие значения э. д. с. или тока в начальный момент (с которого начинается рассмотрение процесса изменение э. д. с. или тока), называются начальными фазами.
Важно понять, что определяя сдвиг по фазе между двумя э. д
с. или токами, нужно всегда определять его между одинаковыми фазами рассматриваемых величин. Например, сдвиг α между нулевыми фазами (рисунок 7, а) и между фазами в Т/5 (рисунок 7, б) одинаков.
Рисунок 7. Определение величины сдвига фаз
Если нужно определить, опережает одна синусоида другую или отстает от нее, поступают следующим образом.
Через нулевую фазу 1 одной синусоиды (ax) проводят вертикаль 1–1 до пересечения со второй синусоидой (by) (рисунок 8, а). Если вертикаль пересекает синусоиду выше горизонтальной оси, значит вторая синусоида опережает первую; если ниже – отстает. Действительно, вертикаль 1–1, проведенная через нулевую фазу синусоиды ax, пересекает by выше горизонтальной оси и, стало быть, by опережает ax. Но если by опережает ax, то ax отстает от by. В этом легко убедиться, проведя вертикаль 2–2 (рисунок 8, б) через нулевую фазу by, которая пересекает отстающую синусоиду ax ниже горизонтальной оси.
Рисунок 8. Определение направления сдвига фаз
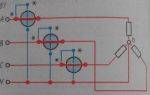
Условные обозначения источников электрической энергии и элементов цепей
| Условное обозначение | Элемент |
|
Идеальный источник ЭДС Е — электродвижущая сила, Е = const Ro = 0 — внутреннее сопротивление |
|
|
Идеальный источник тока I = const Rвн- внутреннее сопротивление источника тока, Rвн>>Rнаг |
|
|
Активное сопротивление R = const |
|
| Индуктивность L = const | |
| Емкость С = const |
К химическим источникам тока относят гальванические элементы и аккумуляторы. В них заряды переносятся в результате химических реакций. При этом в гальваническом элементе реагенты расходуются необратимо, а в аккумуляторе они могут восстанавливаться путем пропускания через аккумулятор электрического тока противоположного направления от других источников.
Источники электрической энергии относятся к группе активных элементов электротехнических устройств. Если Rо=0 и электродвижущая сила (ЭДС) Е=const, то источник называется идеальным. Аккумуляторная батарея по своим параметрам близка к идеальному источнику ЭДС.
К группе пассивных элементов относятся: активное сопротивление R, индуктивность L и емкость С.
В электротехнических устройствах одновременно протекают три энергетических процесса:
1 В активном сопротивлении в соответствии с законом Джоуля — Ленца происходит преобразование электрической энергии в тепло.
Мощность, по определению равна отношению работы к промежутку времени, за который эта работа совершается. Следовательно, мощность тока для участка цепи
p = A/t = ui
Полная мощность, вырабатываемая генератором, равна
где R- полное сопротивление замкнутой цепи, называемое омическим или активным;
Р, I — мощность и ток в цепи постоянного тока.
р, i, и — мгновенные значения активной мощности, тока и напряжения в цепи переменного тока,
g — активная проводимость или величина, обратная сопротивлению g=1/R измеряется в сименсах (См).
В соответствии с законом сохранения энергии работа есть мера изменения различных видов энергии. Так, в электродвигателе за счет работы тока возникает механическая энергия, протекают химические реакции и т. д. На резисторах происходит необратимое преобразование энергии электрического тока во внутреннюю энергию проводника.
Если в проводнике под действием тока не происходит химических реакций, то температура проводника должна измениться. Изменение внутренней энергии проводника (количество теплоты) Q равно работе А, которую совершает суммарное поле при перемещении зарядов:
Q = А = uit
Воспользовавшись законом Ома, получим два эквивалентных выражения:
Это и есть закон Джоуля — Ленца.
Если нужно сравнить два резистора по характеру тепловых процессов, происходящих в них, то нужно предварительно выяснить: протекает ли по ним одинаковый ток или они находятся под одинаковым напряжением?
Если по двум резисторам протекают одинаковые токи, то согласно формуле за одно и то же время больше возрастает внутренняя энергия резистора с большим сопротивлением. С таким случаем мы встречаемся, например, в цепи с последовательным соединением резисторов. Последнее обстоятельство следует учитывать при включении в сеть нагрузки (электроплиток, утюгов, электродвигателей и т. д.). Сопротивление подводящих проводов при этом должно быть значительно меньше, чем сопротивление нагрузки. При несоблюдении этого условия в проводах выделится большое количество теплоты, что может привести к их загоранию.
Если же оба резистора находятся под одинаковым напряжением, то согласно формуле быстрее будет нагреваться резистор с меньшим сопротивлением. Такой эффект, в частности, наблюдают при параллельном соединении резисторов.
Термин «сопротивление» применяется для условного обозначения элемента электрической цепи и для количественной оценки величины R.
Сопротивление измеряется в омах (Ом). 1 Ом — это сопротивление проводника, сила тока в котором равна 1 А, если на концах его поддерживается разность потенциалов 1 В:
1 Ом = 1 В/1 А
Электрическое сопротивление R материалов с изменением температуры меняется. Сопротивление металлических проводников линейно возрастает с температурой. У полупроводников и электролитов с увеличением температуры удельное сопротивление уменьшается, причем нелинейно.
Для сравнения проводников по степени зависимости их сопротивления от температуры t вводится величина a, называемая температурным коэффициентом сопротивления. Отсюда
Для практических расчетов в электрических цепях величину R можно принимать постоянной. В этом случае зависимость напряжения на сопротивлении R от силы тока (вольт-амперная характеристика) будет называться линейной. Электрические цепи, в которые включены постоянные по величине сопротивления, также будут линейными.
Частота
Число циклов изменения параметров переменного тока за единицу времени называется частотой. Частота переменного тока в электросети составляет 50 Гц, то есть за одну секунду он совершает 50 колебаний, каждое из которых состоит из двух полуволн синусоиды.
С повышением частоты наблюдаются следующие явления:
- снижается опасность переменного тока для организма. На заре прошлого века ученый-изобретатель Н. Тесла проводил публичные опыты, в ходе которых пропускал через себя ток напряжением в миллионы вольт (держал за цоколь лампу и она при этом светилась). Ток не причинял вреда потому, что его частота исчислялась в мегагерцах. Частота в 50 Гц принята для сетевого тока по техническим причинам. При такой частоте ток для организма крайне опасен;
- уменьшаются габариты трансформаторов. Данное обстоятельство помогло существенно сократить размеры сварочных аппаратов. Современные модели оснащены инвертором (их так и называют — инверторные) — особой схемой, повышающей частоту тока с 50 Гц до 80 кГц. В результате требуется намного меньший трансформатор, к тому же потери в нем существенно снижаются.
Однако, с увеличением частоты сильнее проявляется поверхностный эффект.
Синусоидальный ток
Наиболее распространён в электротехнике синусоидальный ток. Это периодический переменный ток, изменяющий по закону синуса
i = Im· sin(ωt + ψ),
где i – значение тока в любой момент времени t;
Im– мгновенное значение синусоидального тока;
ω = 2πf = 2πfT, где ω– угловая частота; ψ – начальная фаза переменного синусоидального тока (фаза в момент времени t= 0).
Наибольшее положительное или отрицательное значение переменного тока называют амплитудой.
График переменного синусоидального тока представляет собой синусоиду.
Два синусоидальный тока совпадают по фазе, если они одновременно достигают максимальных и нулевых значений. Если же их фазы различны, то говорят, что токи сдвинуты по фазе.
Наиболее широко в электротехнике применяется трёхфазный ток. Трёхфазная система состоит из трёх однофазных электрических цепей. Электродвижущие силы, действующие в каждой из них, имеют одинаковую частоту, но сдвинуты по фазе относительно друг друга на 120.
В электротехнике однофазную электрическую цепь, входящую в состав многофазовой цепи называют фазой. Если все фазы электрически соединены между собой, то такую систему называют электрически связанной. Фазы в трёхфазной системе могут соединяться «треугольником», «звездой с нейтральным проводом» и «звездой без нейтрального провода».
Если мы сложим все мгновенные значения (положительные и отрицательные) переменного синусоидального тока за период, то получим алгебраическую сумму, равную нулю. Но в таком случае и среднее значение тока также равно нулю. Следовательно, это значение нельзя использовать для измерения синусоидального тока.
Как же определить величину переменного синусоидального тока?
Переменный синусоидальный ток, как и постоянный, обладает тепловым действием. Сравнив его тепловое действие с тепловым действием постоянного тока, можно судить о его величине.
Согласно закону Джоуля-Ленца количество теплоты Q, выделяемое на участке электрической цепи за время t при прохождении тока, определяется следующей формулой:
Q = I2Rt,
где I – величина тока; R– электрическое сопротивление.
Если два тока, постоянный и переменный, протекая через одинаковые по величине сопротивления, за одинаковое время выделяют одинаковое количество тепла, то они считаются эквивалентными по тепловому действию.
Величина постоянного тока, который произвёл такое же количество теплоты, что и переменный ток за такое же время, называется действующим значением переменного синусоидального тока.
Величина действующего значения синусоидального тока связана с его амплитудой соотношением:
Перспективы совместного существования переменного и постоянного тока
Ученых и практиков от электротехники давно занимает вопрос соединения воедино положительных качеств переменного и постоянного тока. Подобные решения стали возможны, благодаря появлению мощных импульсных полупроводниковых вентилей. Сегодня ни у кого не вызывают удивления инверторные устройства, преобразующие постоянное напряжение в переменное, промышленной частоты, и наоборот. Импульсные источники питания в радиоэлектронной аппаратуре и компьютерной технике стали компактными и мощными, в десятки раз более эффективными по сравнению с источниками питания на обычных трансформаторах.
Не менее впечатляющими достижениями импульсной техники могут похвастаться производители источников бесперебойного питания, сетевых импульсных стабилизаторов напряжения, систем получения электроэнергии от альтернативных источников с возможностью аккумулирования и последующего преобразования запасенной энергии при возникновении потребности. Возможности импульсной техники изучены и использованы далеко не полностью. Мы в самом начале этого пути единения постоянного и переменного тока. Совсем не за горами автомобили на электричестве и прочие чудеса, которые станут явью с внедрением новых открытий и разработок в области импульсных источников электроэнергии.
Переменный электрический ток
(AC, аббревиатрура от англ. alternating current) — это меняющийся по своей величине и направлению с определенной периодичностью электрический ток. В электротехнике в качестве буквенного обозначения электрического тока принято использовать знак тильда (~).
Источниками переменного электрического тока служат генераторы переменного тока, создающие переменную электродвижущую силу, изменение величины и направления которой происходит через определенные промежутки времени.
Основные параметры переменного тока
Для его описания используют следующие параметры (см. график):
-
Период (T)
— длительность времени в течение которого электрический ток совершает один полный цикл изменений, возвращаясь к своей начальной величине; -
Частота (f)
— параметр, определяющий количество полных колебаний электрического тока за одну секунду, единица измерения — 1 Герц (Гц). Так, напр. стандарт частоты тока, принятый в отечественных энергосистемах составляет 50 Гц или 50 колебаний в секунду. -
Амплитуда тока (Im)
— максимальное достигаемое мгновенное значение величины тока за период, как видно из представленного графика — высота синусоиды; -
Фаза
— состояние переменного синусоидального электрического тока: мгновенное значение, изменение направления, возрастание (убывание) в цепи. Переменный ток может быть как однофазным, так и многофазным.
Наибольшее распространение получили трехфазные системы, представляющие собой три отдельных эл. цепей с одинаковой частотой и ЭДС, с углом сдвига φ=120°. Более подробно с понятием можно ознакомиться в статье Принцип создания трехфазной цепи переменного тока.
Применение переменного тока
Переменный синусоидальный электрический ток используется практически во всех отраслях хозяйства. Широкое применение переменного тока обусловлено во многом экономической эффективностью его использования в системах электроснабжения, простотой в преобразовании из энергии низкого напряжения в энергию более высокого напряжения и наоборот.
Эта возможность позволяет уменьшить потери электроэнергии при ее передаче на большие расстояние по проводам, существенно снизив площадь их поперечного сечения.